Dans cette vidéo nous allons montrer que deux sous-espaces vectoriels sont supplémentaires par analyse-synthèse. Cette vidéo est la première d’une série de 4.. Sous-espaces supplémentaires. Pour montrer que les sous-espaces vectoriels F et G sont supplémentaires dans un espace vectoriel E, on montre à la fois la somme directe F ∩ G = {0} et le fait qu’ils engendrent l’espace total F + G = E. En dimension finie, il suffit de ne démontrer que deux des trois propriétés suivantes pour obtenir la.

06 montrer que deux droites sont confondues YouTube

Savoir si ESPACES VECTORIELS en SOMME DIRECTE et SUPPLÉMENTAIRES Méthode + Explication

MONTRER QUE DEUX SOUS ESPACES VECTORIELS ÉGAUX YouTube

Savoir si ESPACES VECTORIELS en SOMME DIRECTE et SUPPLÉMENTAIRES 2 Méthode + Explication

MONTRER QUE DEUX SOUSESPACES VECTORIELS SONT SUPPLÉMENTAIRES (UNICITÉ + EXISTENCE) 2 YouTube
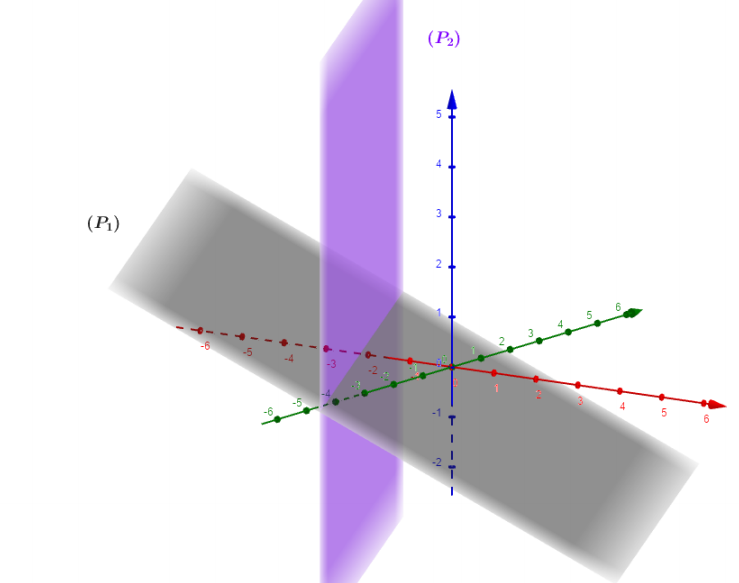
Montrer que deux plans sont parallèles La géométrie dans l’espace et produit scalaire TS J

montrer que deux droites sont coplanaires

Comment montrer que deux droites sont perpendiculaires avec des vecteurs ? Cours de maths

Exercice corrigé.Sur Comment montrer que deux sous espaces vectoriels sont supplémentaires
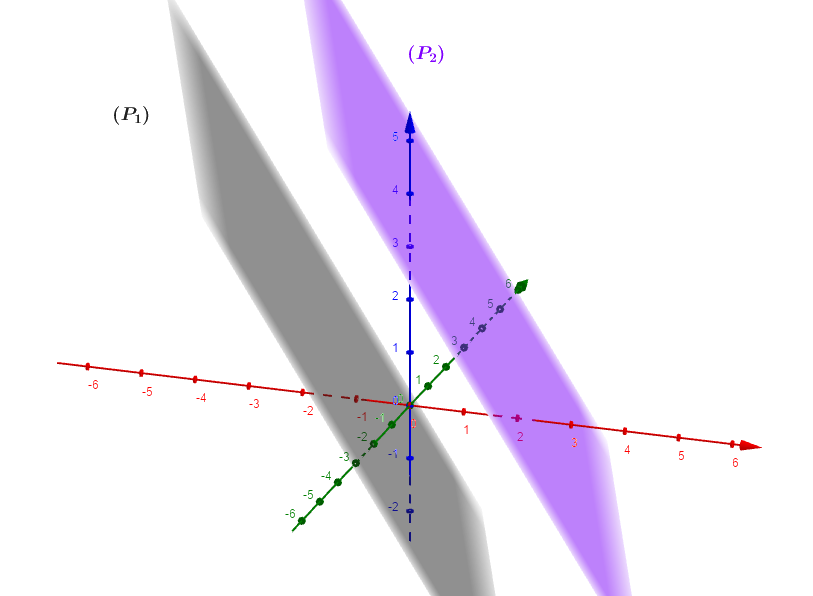
Montrer que deux plans sont parallèles La géométrie dans l’espace et produit scalaire TS J

Sousespaces supplémentaires existence, dimension YouTube
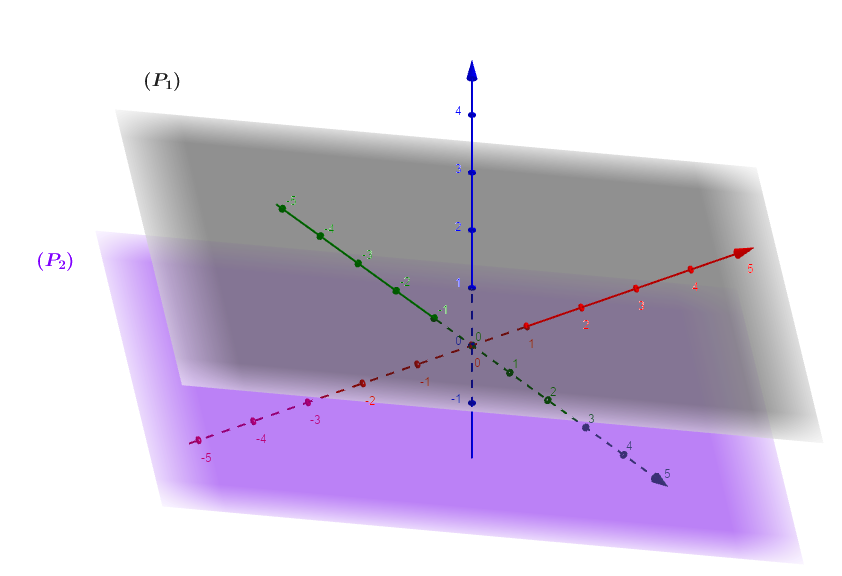
Montrer que deux plans sont parallèles La géométrie dans l’espace et produit scalaire TS J

Exercice Comment savoir si deux vecteurs sont colinéaires ? Terminale YouTube

07 montrer que deux droites sont sécantes YouTube
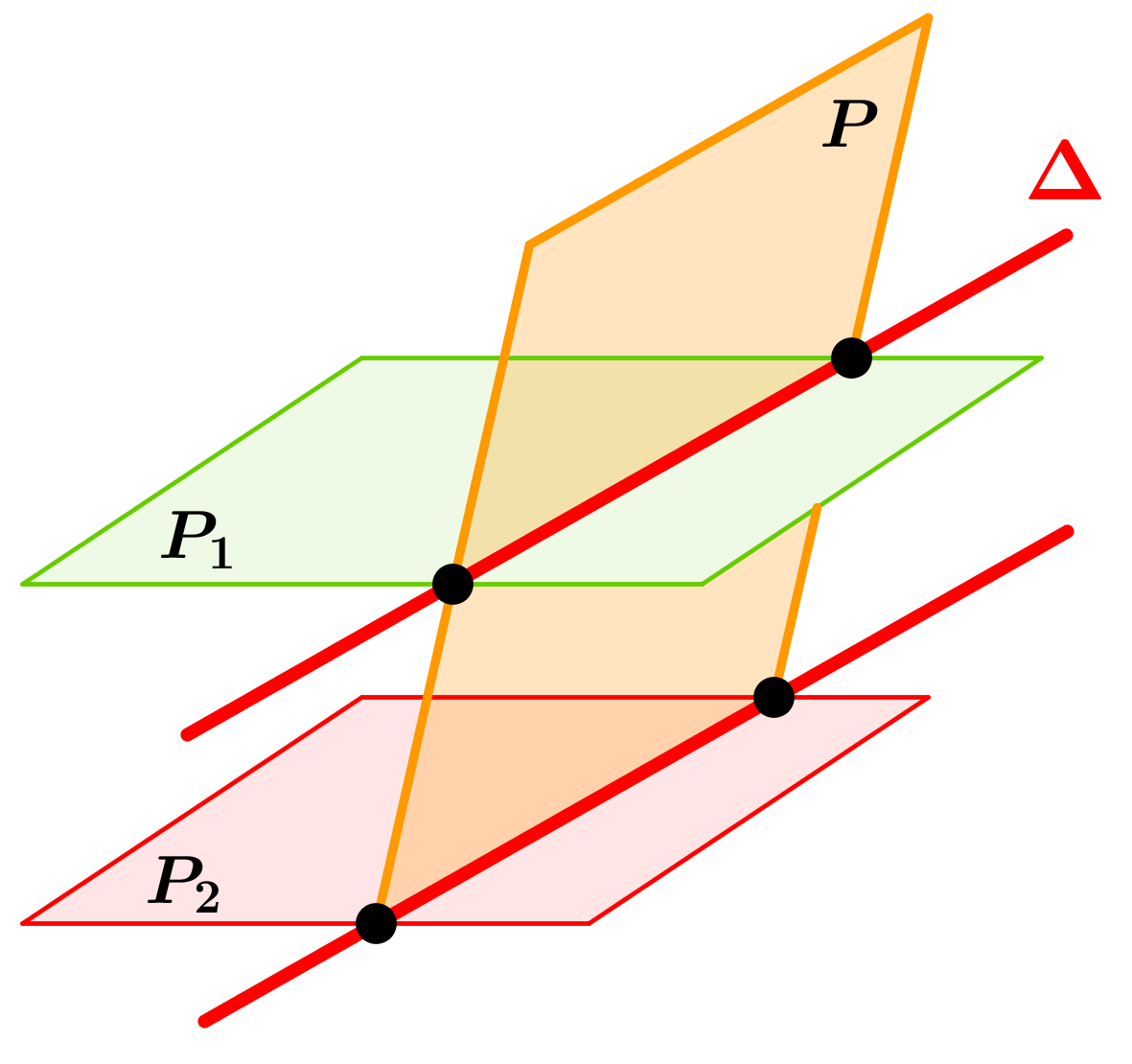
démontrer que deux plans sont parallèles

base d’un espace vectoriel de dimension infinie

Exercice 1.4. Sommes directes et sous espaces supplémentaires YouTube
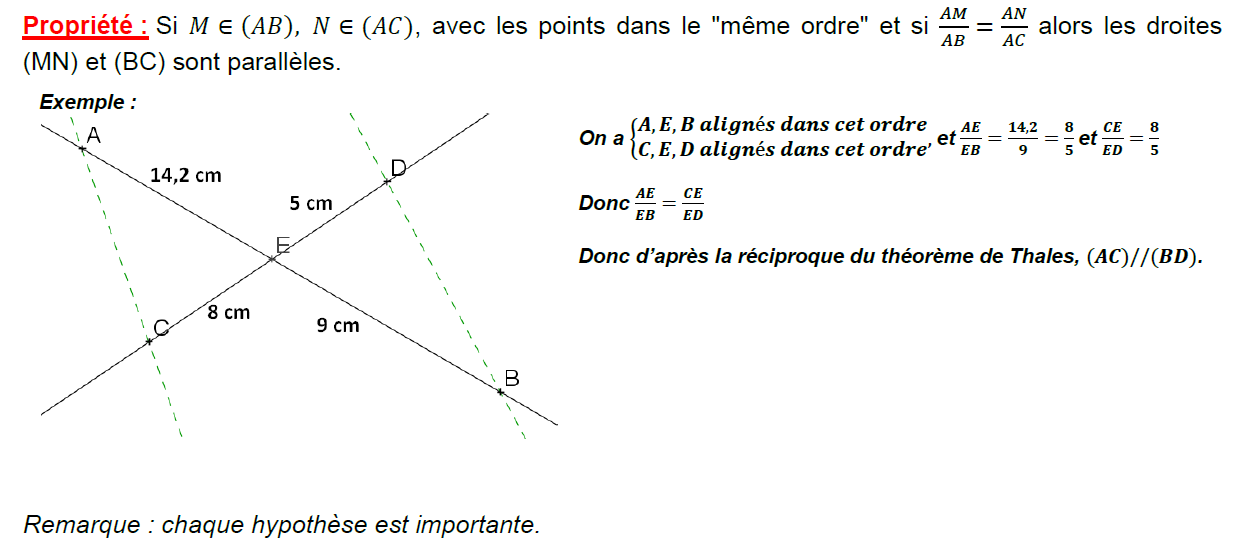
Montrer Que Deux Droites Sont Parallèles Communauté MCMS
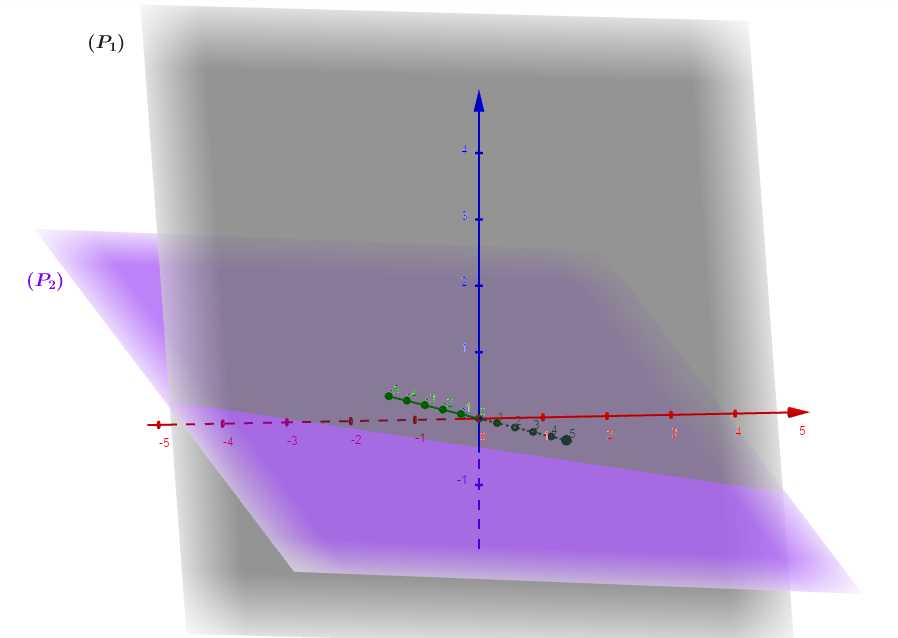
Montrer que deux plans sont parallèles La géométrie dans l’espace et produit scalaire TS J

Espaces vectoriels Exo7
Comment montrer que deux sous-espaces vectoriels sont supplémentaires? Soit F et G deux SEV de E. • Méthode 1: On montre que F G = {0 E} et E = F+G • Méthode 2: On montre que tout élément de E s’écrit de manière unique comme somme d’un élément de F et d’un élément de G. On pourra être amené à raisonner par analyse-synthèse. Grâce à cette vidéo vous saurez montrer que deux ensembles sont des sous-espaces vectoriels, qu’ils sont en somme directe et qu’ils sont supplémentaires.Si t.